The Online Teacher Resource

Email Newsletter

Decimals Worksheets

We have a ton of different worksheets that incorporate the use of decimals in math. These worksheets include basic operations, comparisons, conversions, decimal ranges, and the use of negatives. You would also find our fraction worksheets go along well with this topic.



Addition

Multiplication

Subtraction

Division

Comparisons


What Are Decimals In Math?

Decimals are used in almost every field, including accounting, banking, engineering, taxation, and medicine. They are commonly used to represent portional fractions like tenths and hundredths.

Since these types of values are one of the basic math concepts, it's imperative to ensure your student has a command over them. Due to many digits and a different way to read these form of values, operations on decimals become tricky.

With real-life examples and gradually building up the concept, your students can quickly grasp this complex concept of decimals and understand the diferent forms of them.

What Are They?

Decimals are a way to write fractions with a denominator of 10 or a multiple of 10. They help students understand the base-ten number system and the relationships between numbers.

These values are essentially a number written with a dot, or dotted point, representing the division of one whole number by another.

Here’s an example to clarify how we use these values in our daily life.

A summer camp is usually two weeks long. If we use this type of way to measure the time that has passed over these two weeks, each week would be equal to 0.5 (1⁄2) or 50 percent of the total length of camp. We will reach this result because there are 2 weeks in the whole summer camp session. Each day would be worth 1⁄10 (0.1) or one-tenth of the entire session because there were 10 days in 2 weeks.

Teaching This Skill

Teaching decimal place value is a challenging task. Use the place value chart to help your students visualize this concept in places and values. A decimal is a fractional part of a whole number, and the location of the precise point in a number determines the value of each digit.

Decimal Place Value Chart


Value Chart

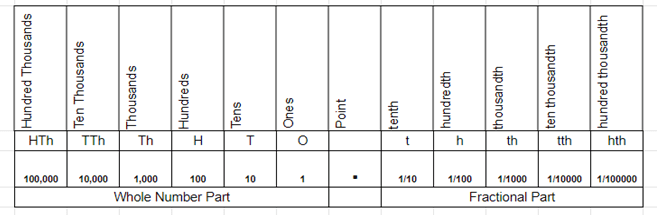
Align the dot within the decimal number with the point in the chart and then find the value.

For example, the value of 3 in the number 1.34 is tenths.

The Different Types

There are two types: Terminating and non-terminating. Non-terminating are further divided into two: Recurring and non-recurring decimals.

Terminating

Any decimal number that ends or terminates and has a finite value representation is called a terminating form. You can tell how many digits to the right of the decimal point there are in any terminating decimal number just by looking at it. For example: 1/2 = 0.5, 1/4 = 0.25, 10/8 = 1.25, 3/10 = 0.3, 5/16 = 0.3125, etc.

Non-Terminating

Any decimal number that doesn't end or terminate and has a infinite representation is called a non-terminating version. You can’t tell how many digits to the right of the delinated point there are in a non-terminating decimal number. For example: 1/3 = 0.3333333, 4/15 = 0.2666666, 12/9 = 1.3333333, 6/88 = 0.06818181818, etc.

Recurring

Sometimes, you will come across a non-terminating decimal that repeats the same pattern. For example, 0.333333333…. In this case, the digit three in this figure repeats endlessly, which is called a recurring form.

Recurring decimal get their name from the fact the number keeps repeating itself infinitely. You can represent these types of values by placing dots above the numbers that repeat themselves: 0.3... . You might also see it written like this: 0.(3).

Non-recurring

A non-terminating value that does not repeat the same pattern. For example, 22/7 is 3.141 592 653…. In this case, there’s no pattern of repetition. This is called a non-recurring decimal.

Such values are usually calculated to three places and are then rounded off.

Properties of Decimals

In arithmetic, there are numerous properties of numbers. However, we're only consulting the three most essential properties concerning multiplication and addition of decimal numbers.

Multiplicative Properties

Property

Description

Example
Commutative Property

The product of decimal numbers remains the same even if the order of decimal numbers changes.

3.5 x 2 = 7

2 x 3.5 = 7
Associative Property The product of decimal numbers remains the same even if the groups of decimal numbers are shuffled.

3.5 x (2 x 4) = 28

(3.5 x 2) x 4 = 28

Additive Properties of Decimals

Property Description Example
Commutative Property

The sum of decimal numbers remains the same even if the order of decimal numbers changes.

3.5 + 4.2 = 7.7

4.2 + 3.5 = 7.7
Associative Property The sum of decimal numbers remains the same even if the groups of decimal numbers are shuffled.

3.5 + (4.2 + 1.1) = 8.8

(3.5 + 4.2) + 1.1 = 8.8

Distributive Property

The distributive property of decimal numbers includes both multiplication and addition.

If two decimal numbers are added, and their sum is multiplied by a number, the answer will be the same if the two decimal numbers are first multiplied by the said number, and then their products are added.

Example:

4 (1.2 + 1.8) = 4 (3.0) = 12

4 x 1.2 + 4 x 1.8 = 4.8 + 7.2 = 12.0

Conclusion

Decimals are ubiquitous. Whether it's a hair color we want to buy or the score you give your students, everything has the usage of decimals. Therefore, knowing about decimals is crucial for students.

When solving problems, a visual guide such as a decimal place value chart will come in handy for students that you can gradually prohibit.

Allow students to ask questions but encourage them to find answers independently or through peer work. Teaching your students decimals will provide them a solid foundation for further understanding other mathematical principles. Therefore, your role as a teacher who's providing these foundational lessons matters.