An Overview of Basic Trigonometry, Trigonometric Equations, and Some of its Applications
Literally, trigonometric equations concern themselves with "triangle measurement"; and trigonometry is a specialized branch of mathematics that deals mainly with the properties of triangles and the relationships between its parts. The Basic Trigonometry course discussed in high schools and colleges is concerned with the Euclidean triangle (a triangle whose sum of all its angles is equal to 180 degrees).
Trigonometric Ratios
Trigonometry relies heavily on what we call trigonometric ratios. First, let us examine a right triangle (a triangle with one right angle for the uninitiated). The hypotenuse is the longest side of the right triangle; the other two sides are the legs. For the acute angle A on the right triangle below there is an adjacent side (a leg contained on angle A) and an opposite side (a leg not contained on angle A). In triangle ABC as shown:
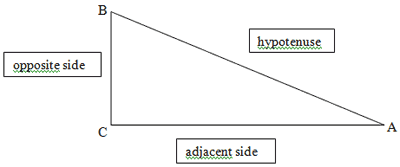
The six trigonometric ratios are the sine, cosine, tangent, cotangent, secant, and cosecant. They are defined as follows:

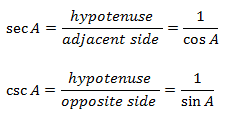
Note that the cotangent, secant, and cosecant are just the respective reciprocals of the sine, cosine, and tangent. So, once you remember the sine, cosine, and tangent, you can know the values of all other three ratios. In high school discussions, there is a famous mnemonic dealing with this: SOH - CAH - TOA: sine (opposite side/hypotenuse); cosine (adjacent side/hypotenuse); tangent (opposite side/adjacent side).
Trigonometric ratios can also be extended by basing them from the unit circle (a circle with center at the origin and radius equal to 1).
Trigonometric Identities
Trigonometric identities are statements that always hold true for some given parameters. All of the following trigonometric equations frequently emerge in trigonometric problems and should be memorized. The most usable trigonometric identities are as follows:
The Pythagorean Identities
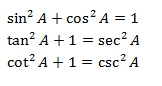
Reciprocal Identities (shown already)
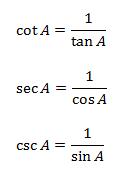
Sum and Difference Identities
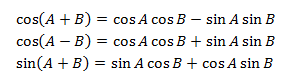
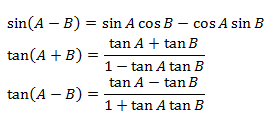
Double Angle Identities
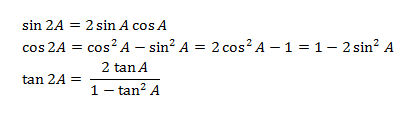
Half-Angle Identities
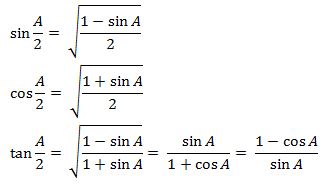
More on Triangles
The most fundamental theorem concerning triangles is the Pythagorean theorem, which states that the sum of the squares of the legs of a right triangle is equal to the square of the length of the hypotenuse. Many of us have heard repeatedly: a2 + b2 = c2. There are other important formulae concerning triangles that should be memorized:
Sine Law
In triangle ABC, if AB = c, BC = a, and CA = b, then
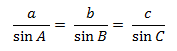
Cosine Law
In triangle ABC, if AB = c, BC = a, and CA = b, then
![]()
The sides and angles in the cosine law are also interchangeable, as follows:
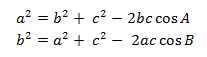
Note that in the cosine law, when the angle on the right side of each equation is equal to 90O (cos 90° = 0), it reduces to the Pythagorean theorem.
Trigonometry textbooks often present plenty of realistic problems involving trigonometry. Basic trigonometry is often applied in astronomy, where trigonometric ratios are used to measure the distances between large bodies using known distances of heavenly bodies; geography, where large distances between places in the world can be computed using already known distances; and navigation, where ships and airplanes use trigonometric ratios to determine their precise locations. Many of the problems invoke the concepts of angle of elevation, angle of depression, and bearing. In these settings is necessary to understand the problem before proceeding to draw a suitable figure.
More advanced applications of trigonometric equations involve the Fourier series (an infinite sum that involves plenty of trigonometric ratios) that has plenty of uses in engineering, seismology, acoustics, and in many other advanced topics in mathematics; and Fourier transforms (which contains integrals instead of infinite sums) that concerns itself with the rates of change of many physical phenomena (like population growth and resonance) and thus, require calculus.